In serious navigation projects, analog inertial sensors must be preferred instead of sensors with digital outputs. Some form of analog to digital converter (ADC) is required in order to read the outputs from these analog sensors.
Selection of a proper ADC by itself is a serious topic. Essentially, ADCs can be categorized into 3 classes:
- Sequential ADCs
- Flash ADCs
- Sigma-Delta ADCs (Over Sampled ADCs)
(For a complete review of ADC technology, I suggest everyone reading Analog Devices’ ADC handbook). Sequential and Flash ADCs are fast but have a low resolution. In order to sample a gyroscope with a resolution of 24bit or more, a sigma-delta ADC (ΣΔ ADC) has to be used.
ΣΔ converters internally sample the analog inputs using a 1 bit ADC with a very high rate (that is why they are called as over-sampled ADC). After 1bit sampling operation, these 1bit samples are processed with a digital filter (and downsampled) to generate high resolution samples of the analog input. The digital filter used in ΣΔ ADC has a low pass characteristic. Therefore, ΣΔ ADCs cannot be used for high BW signals.
High speed and high resolution ΣΔ ADCs with simultaneous multiple channels can be very expensive. (they can cost more than 200$). Therefore, IMU designers who use this traditional approach find themselves in a situation in which they have to make a compromise between speed and resolution.
Having summarized the traditional approach, I can start attacking and blaming everyone who blindly follows this approach.
The main point that these people fail to understand is that we never need acceleration and rotation rates to solve the INS equations. All we need is the integral of these quantities (a.k.a angle and velocity increments). In this case, why don’t we integrate the signal with an analog front-end and then sample only this integral value? Or, even better, why don’t we use a front-end which integrates and samples the rate signal at the same time so that we don’t bother ourselves with integrating the signal (either in digital or analog domain) at all?
Here is a block diagram of such a circuit that can be used to integrate and digitize analog signals. It is in fact nothing but the simplest form of an ΣΔ modulator. Despite its simplicity it accomplishes exactly what we need.

The first summation junction is used to add sensor outputs when more than 1 inertial sensor is used per axis (i.e. orthogonal redundant configurations). Redundancy is a life saver. I strongly recommend everyone to use it even if only 1 sensor per axis is used. The feedback loop is a sigma-delta modulator. The 1 bit ADC is essentially a comparator. The feedback loop stabilizes the integrator output at “0”. Without such a feedback loop, the capacitor would not operate in the linear region. The 1 bit DAC generates either Vmax or 0 (we assume that sensor outputs changes only in the range of [Vmax 0]). The clock of the D flip-flop determines the time support of each rectangular pulse generated by the 1bit DAC. When the output of the latch (D flip flop) is high, the counter increments. Thus, the counter output is equal to the integral of the feedback signal. Therefore, it approximates the integral of the input. Thanks to the feedback loop, the maximum error on this integral is equal to dt*Vmax where dt is the period of the clock. Therefore, the faster is the clock, the better is the approximation. Regardless of the total integration time the error is bounded by this value. (In rate sampling systems the integral error keeps increasing in time without a bound. That is why we need very high BW to reduce the integration errors in rate sampling structures). Even if a moderate clock is used (e.g. 1Mhz) this error becomes completely negligible with respect to any other error source. Therefore, this integral sampling method can safely be assumed errorless.
The following figure shows a very primitive circuit which realizes the above block diagram. It assumes that the analog signal varies between Vmax and “0”. An analog designer would probably laugh at the simplicity of this circuit (no op-amp bias current compensation, no voltage isolation etc). But still, I suppose it will work as intended.
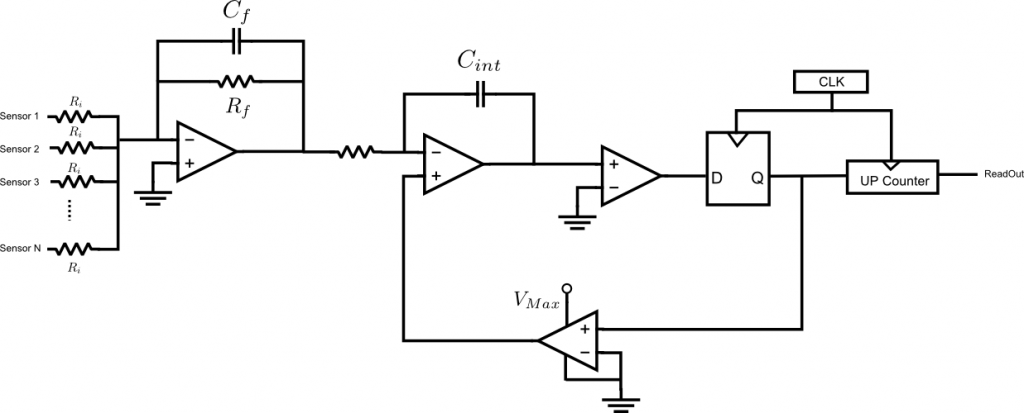
As a result, the approach described above has 2 distinct advantages which make it superior to any ADC based approach:
- The quantization errors on the angle and velocity increments computed with this circuit is negligible.
- A rate sensor must be sampled very fast in order to minimize the errors on the integrals. The above circuit computes the integrals in the analog domain. You only need to read the counter output whenever you need the angle/velocity increment values. Therefore, it provides a great flexibility on the timing requirements.
